Nur damit ich das später mal wieder finde, wenn ich es das nächste Mal brauche hier ein paar lustige Ressourcen zum Einheitskreis und Trigonometrie die man sonst nur schwer im Netz findet.
Bekloppte Mathematiker
Wer sich mal näher mit Kreisberechnungen beschäftigt, i.e. im Bereich der Programmierung, der schlägt die Hände über dem Kopf zusammen, wie kompliziert die Programmierbeispiele für diesen Kram sind.
Und das liegt an ZWEI schlimmen Dingen die Mathematiker offenbar cool, oder nicht so schlimm finden:
- Mathematiker finden nichts Schlimmes daran, ständig für die Kreisberechnung einen Basiswert von 2? (Zwei Pi) überall hinzurotzen, statt einfach ? = 2? (Tau gleich Zwei Pi) zu definieren, damit man eine schöne bezugszahl für den Vollkreis hat. (Das schlägt übrigens auch Physiker @mhartl vor auf tauday.com.)
- Alle dämlichen Codebeispiele werden in Radians bzw. dem Bogenmaß des Einheitskreises gerechnet, statt in Degrees bzw. Grad unter denen sich ein normaler Mensch was vorstellen kann.
Aus diesem Grund habe ich meinen Programmcode so gestaltet, dass er immer in Grad rechnen kann und mit ? (Tau) wobei ich für ? (Tau) als Wert 2? (Zwei Pi) definiere. Wenn man mit durchgehenden 360 Grad eines Vollkreises rechnet, fallen nämlich bequemerweise alle komischen Vorzeichenwechsel von komischen Radianswerten weg, die man sonst üblicherweise als Nebenwirkung hat.
Einheitskreise
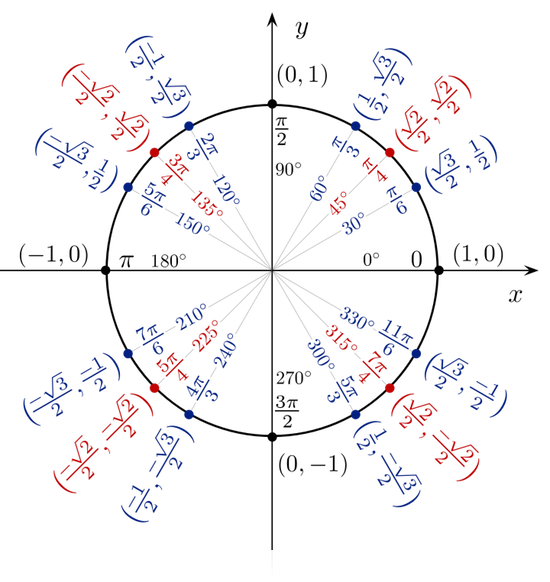
Quelle: Wikipedia
Hier mal eine grafische Übersicht der klassischen Lehre vom Einheitskreis mit den ganzen komischen Dingen die man da bekommt. Rechts der Einheitskreis mal in Quadranten aufgeteilt, denn diese doofen Quadranten muss man beachten für einige Berechnungen, wenn man nicht mit dem Vollkreis rechnet (Quelle: „Polar and Cartesian Coordinates“, bei MathIsFun.com).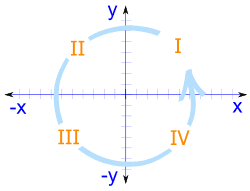
Polarkoordinaten
Eigentlich will man auf dem Kreis immer nur seine Position bestimmen wenn man mit dem Ding rechnet oder andere Dinge die von dieser Position abhängen, z.B. Winkel zwischen Strecken und Längen von Strecken. Primitivere Anforderungengibts also eigentlich gar nicht. Ich hab einen Kreis und ich hab irgendeine Position auf dem Kreis (nennen wir die mal einen Punkt) und ich will z.B. wissen welchen Winkel eine Linie zur horizontalen (x-Achse) hätte, die ich vom Kreiszentrum zu dem Punkt führe. Simple Frage, oder?
Und das kann man ausrechnen. Es ist sogar eine nicht sehr unübliche Berechnung. Nein, es ist sogar die häufigste Berechnung, die man am Kreis ausführt. Man nennt diesen Winkel auch die Polarkoordinate. Wenn ich sage meine Position ist bei 45° auf dem Kreis, gibt es keine Missverständnisse. Es ist eine eindeutige Koordinate, die man gerne mit ? (Theta) bezeichnet. Da ist es übrigens auch völlig schnuppe wie große der Kreis ist bzw. welchen Radius r der hat. Erst wenn ich die Koordinate auf einem anderen Kreis beschreiben will, muss ich auch den Radius r beachten und den als Teil der Koordinate auffassen. Hat man nur einen Kreis ist die Sache also schön einfach!
Weil Mathematiker aber so richtig große Arschlöcher sind, dass sie Zeug halt gerne komplizierter schreiben als nötig, nehmen die halt gerne griechische Buchstaben von denen keine Sau weiß wie sie heißen, oder wie man sie ausspricht. Das schützt das Herrschaftswissen der Mathematiker. Sonst könnte das ja sofort jeder verstehen und benennen, das wollen Mathematiker natürlich nicht, dann wären sie ja nichts Besonderes mehr. Lerne, wenn man Menschen die Fähigkeit nimmt etwas zu benennen, können sie damit auch nicht vernünftig arbeiten. Toll, oder? Hier kann die Politik noch von der Mathematik lernen. Einfach eine eigene Geheimsprache zulegen!
Alternativ könnte ich übrigens ausrechnen, wie weit der Punkt vom Zentrum horizontal (x-Achse) entfernt ist und wie weit er vertikal (y-Achse) entfernt ist. Das sind dann aber zwei Zahlen die ich brauche, um die Position in einem zweidimensionalen (kartesischen) Koordinatensystem zu beschreiben. Ein X- und ein Y-Wert. Ist natürlich für die Programmierung deutlich einfacher, wenn man nur mit einer Zahl zu tun hat, statt mit zweien, daher sind Polarkoordinaten eine tolle Sache.
Dämlich ist bloss, Computer können ihren Bildschirm nur in kartesischen Koordinaten ansprechen. Ich muss die tolle Polarkoordinate also oft wieder umrechnen, sobald ich da konkret was auf dem Bildschirm darstellen möchte. Deshalb konvertiert man oft zwischen beidem Zeug hin und her, wenn man das nicht einfach macht eine schöne Quelle für Fehler.
Es geht aber in einfach: Das wird bloß gerne geheimgehalten von Mathematikern & Informatikern, denn die sitzen ja beide im selben Boot. Das Geheimnis heisst atan2(x,y). Eine Geheimfunktion, die einen X- und Y-Wert nimmt und diesen in eine Polarkoordinate umrechnet (natürlich in Radians, sonst wäre es zu einfach). Und damit das keiner sofort findet, haben die das schön in einem eigenen Wikipedia-Artikel versteckt.
Polarkoordinaten, kartesische Koordianten in Bogenmaß und Grad
Da eine Fehlerquelle allein langweilig ist, hat man sich noch ausgedacht beim Programmieren alle Standardfunktionen der Trigonometrie (sin, cos, tan, cot) nur im sogenannten Bogenmaß bzw. Radians rechnen zu lassen. Die geben einem also effektiv falsche Werte geben, wenn man da Werte in Grad, also einen Winkel von ? = 45° reintut. Und ganz egal was man reintut, raus kommt immer nur Bogenmaß also Radians.
Das haben sich die Entwickler der Programmiersprachen ausgedacht, die sind häufig die gleichen Arschlöcher wie die Mathematiker, oft sogar in der gleichen Person. Die wollen also nicht, dass jeder mal eben mit den tollen Funktionen rechnen kann. Das sollen nur Spezialexperten können, daher hat man das im sogenannten Bogenmaß-only gemacht. Es gibt also keine Sinusfunktion in deiner Mathematikbibliothek deiner Programmiersprache, die als Eingabewert Werte in Grad akzeptiert. Da haben die Mathematiker und Informatiker nämlich was dagegen.
DESHALB muss man für jede kleine Scheißrechnung vorher die Einheit von Grad in Radians umrechnen. Und das was dann da rauskommt (z.B. aus einer atan2(x,y)-Funktion) ist auch im Zweifel wieder ein Radians-Wert mit dem keine Sau was anfangen kann ausser halt der Computer. Joa, so macht man sich das Arbeiten schwer würde ich sagen. Man ist also eigentlich immer nur am Konvertieren statt am Rechnen.
Fuck 2?
Eine besondere Kuriosität ist übrigens, dass die Mathematiker so bekloppt sind, dass die sich bei Kreisberechnungen auf 2? (Zwei Pi) anstatt ? (Tau) beziehen. Denn hey, warum eine Kreisvariable definieren die ? = 2? ist, wenn man so die Sache schön kompliziert aussehen lassen kann? Oh und übrigens haben die Informatiker den Mathematikern auch geholfen dafür zu sorgen, dass griechische Symbole keinesfalls einfach über die Computertastatur eingetippt werden können. Sonst wäre das ja zu schnell irgendwo aufgeschrieben.
Oh, und selbst wenn man das tippen kann, haben die Datenbankprogrammierer und die Programmierer von WordPress in seltener Einigkeit dafür gesorgt, dass getippte griechische Symbole keinesfalls mal eben so gespeichert werden können. Deshalb haben sie für die Datenbank per Default ASCII statt UTF8 benutzt. Daher sind die Symbole hier auch alle nicht lesbar, sie sind schlicht nicht gespeichert und nicht speicherbar. Aber irgendein abtrünniger Informatiker oder Mathematiker hat die griechischen Symbole tatsächlich irgendwann in HTML definiert damit er vermutlich sein Geheimwissen in geheimen Internetseiten ausdrücken kann. Ich rufe laut und deutlich KETZER!!!!! Ich kann also mit der Hilfe dieses Abtrünnigen Verräters die Zeichen
- θ (Theta)
- τ (Tau)
- π (Pi)
trotzdem schreiben, was für eine Schande für die Zunft.
Daher noch einmal in groß:
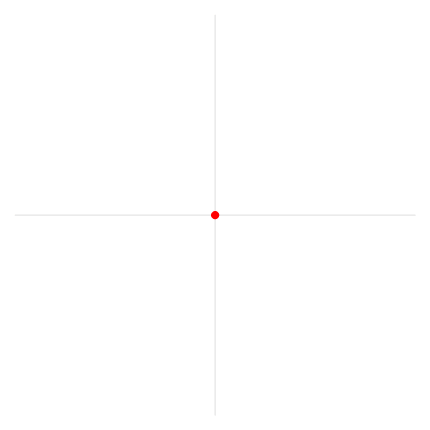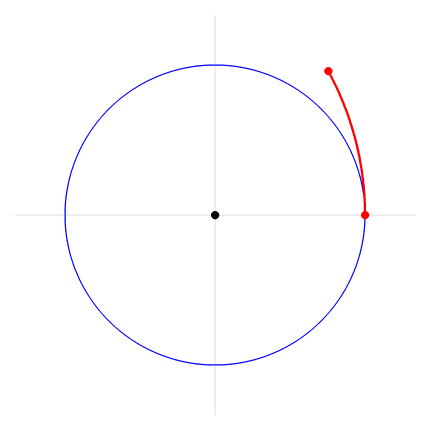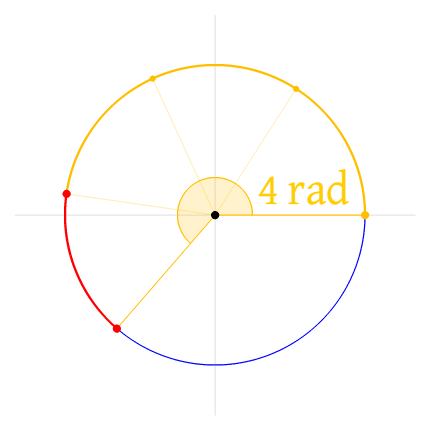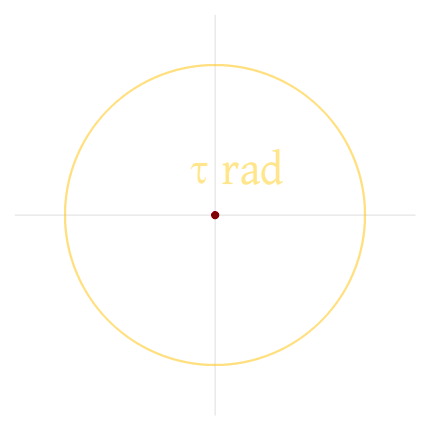
Source: http://tauday.com/state-of-the-tau
Und bitte liebe Objective-C und bald Swift-Programmierer. Lasst den Scheiß Leute auf eure tollen selbstdefinierten precompiler-Hacks auf Stackoverflow hinzuweisen, um von Grad in Radiant umzurechnen. Dafür gibt es Funktionen die bereits an Bord sind. Und die heißen:
GLKMathRadiansToDegrees
Weitere nützliche Seiten:
Tau Propaganda
I just found…
A black & white summary sheet highlighting key tau facts with relevant sources for the curious.

as PDF and as HQ image.
Oh and this one… haha…

Source: xkcd
Why do I blog this? Weil Mathematiker und Informatiker riesige Arschlöcher sind und von Einfachheit bei der Benutzung nichts wissen wollen. Und weil ich mit deren kruden Mist und Funktionen rechnen muss, wenn ich mir nicht meine eigene Trigonometrie-Bibliothek in Grad bauen will. Und weil ich ja nichts Besseres zu tun habe…
